Homepage of Dr. René Wittmann - Department of Theoretical Physics II

Chair Löwen

Dr. René Wittmann
Postdoc

Institut für Theoretische Physik II - Soft Matter
Heinrich-Heine-Universität Düsseldorf
Building 25.32
Room O2.54
Universitätsstraße 1
D-40225 Düsseldorf, Germany

phone: +49-211-81-15934
e-mail: wittmann <at> thphy.uni-duesseldorf.de

Curriculum Vitae

2018-present	Postdoctoral Research Fellow at the Institute for Theoretical Physics II, Heinrich-Heine University Düsseldorf, Germany
2015-2018	Postdoctoral Research Fellow in the Soft Matter Theory group, University of Fribourg, Switzerland
2015	PhD at the Institute for Theoretical Physics I, Friedrich-Alexander University Erlangen, Germany

Publications

Examples of my research are linked below.
A full list of publications can be found on Google Scholar

My research spans between biological, chemical and mathematical physics and focuses on the development, validation and application of microscopic theories for complex soft matter systems.
My favorite tool is classical density functional theory (DFT), which allows for calculating structural and thermodynamical equilibrium properties from first principles and can also be extended to describe dynamical systems.

Mathematical validation of statistical theories

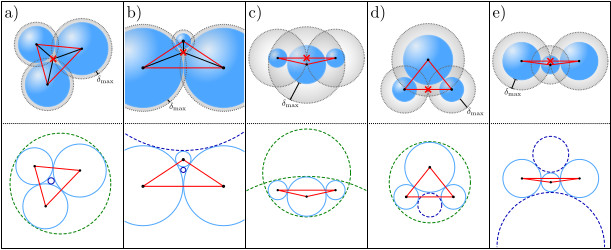
First figure: Rigorous proof of exact depletion pair potentials via Descarte's circle theorem [Preprint].

Foundations of classical density functional theory (DFT)

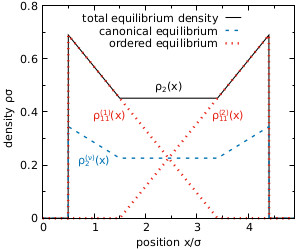
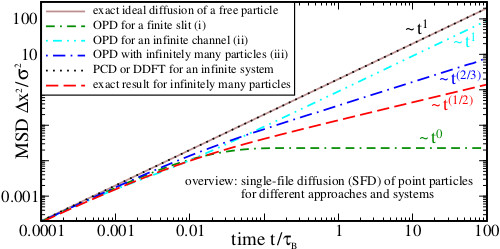
First figure: ergodicity assumption leads to particle exchange in one dimension [PRE (2019)],
Second figure: dynamical DFT based on ordered ensemble predicts subdiffusion [Mol. Phys. (2021)].

Development and application of geometry-based classical density functional theory (DFT)

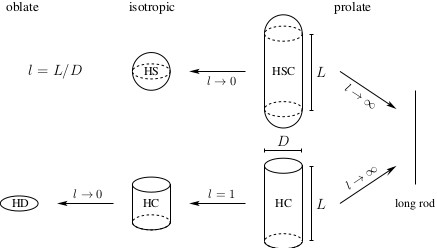
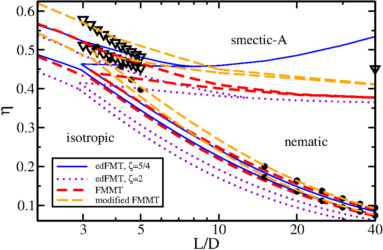
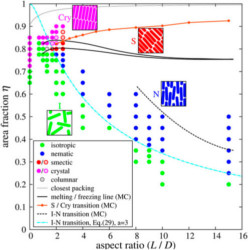
First figure: scaling of hard bodies: the fundamental-measure DFT must describe all limits [JCP (2014)],
Second figure: phase diagram of hard spherocylinders (HSC) in 3d: improving the functional [JPCM (2016)],
Third figure: phase diagram of hard discorectangles (HDR) in 2d: free minimization and analytical isotropic-nematic transition [JCP (2017)].

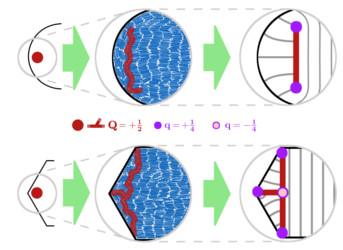
Topology of smectic liquid crystals in complex confinement

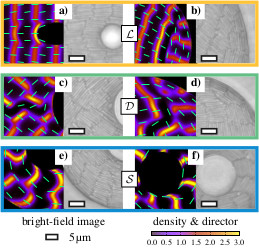
First figure: structural details of smectic states in annular confinement (DFT and experiment) [Nat. Comm. (2021)], [Pressebericht: Flüssigkristalle unter Stress],
Second figure: revealing the topological fine structure of spatially extended defects [PRL (2021)], [Physics Synopsis: Topology Inside a Liquid Crystal].

Modeling biological systems

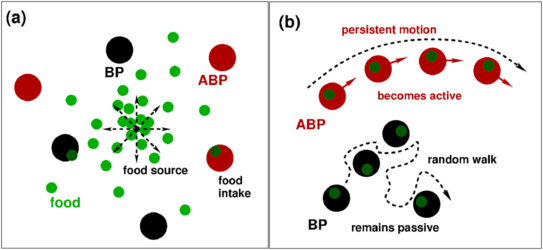
First figure: active Brownian particles (ABPs) activated by food intake [PLOS One (2020)],
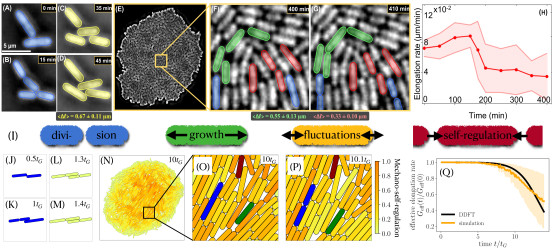
Second figure: growing bacterial colonies [Preprint].

Development and analysis of active particle models

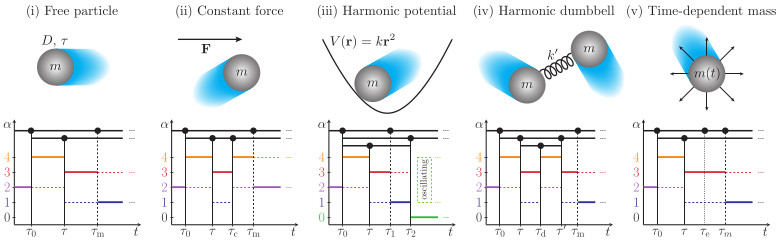
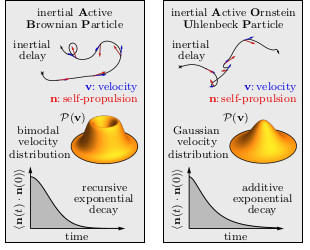
First figure: inertial active Ornstein-Uhlenbeck particles (AOUPs) and a diagram of their dynamic exponents [JPCM (2021)],
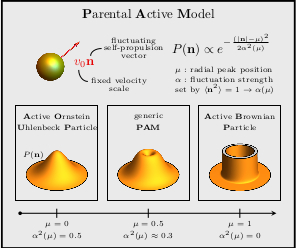
Second figure: unifying ABPs and AOUPs in a parental active model [JCP (2022)],
Third figure: AOUPs with rotational inertia [Preprint].

Collective behavior of active particles close to equilibrium

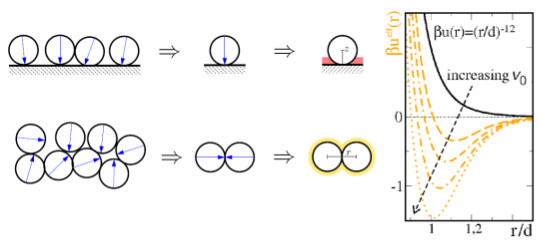
First figure: phenomenology of active particles through effective attractions [JStat (2017)],
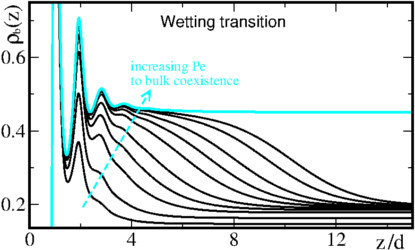
Second figure: activity-induced wetting transition in effective equilibrium [EPL (2016)],
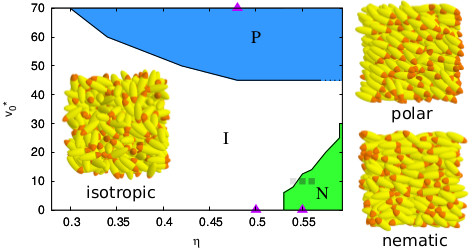
Third figure: activity destabilizes the nematic phase of self-propelled rods [PRE (2018)],
Fourth figure: equilibrium-like relations between pressure, adsorption and surface tension at a curved wall [JCP (2019)].

Dynamics under concurrent external constraints

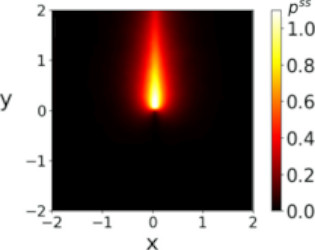
First figure: stationary behavior of a stochastically reset particle under Lorentz force in an inhomogeneous magnetic field [PRR (2020)],
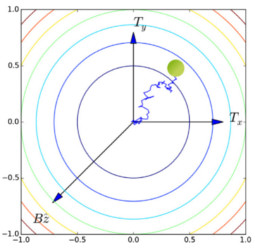
Second figure: multithermostat particle subject to a Lorentz force [New J. Phys. (2020)],
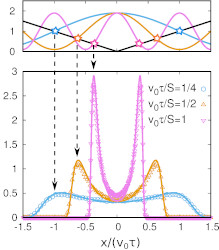
Third figure: space-dependent activity and confinement [SciPost Phys. (2022)].

Commitment information: I accurately check the content of external links, but I do not enter into a commitment for their content. Responsible for the content of linked pages are the operating companies.

Chair Löwen

Curriculum Vitae

Publications

Research