Institut für Theoretische Physik II: Weiche Materie - HHU Düsseldorf
Fortgeschrittenen-Praktikum: Weiche Materie - Archiv - Getriebene Mischung durchdringbarer Kugeln
Getriebene Mischung durchdringbarer Kugeln
Motivation
Die Beschäftigung mit Modellen, die kein experimentelles Pendant
haben, kann trotz dieses Defizits lohnend sein. Zum einen lassen sich theoretische
Methoden an solchen Modellen testen, zum anderen kann man damit einen Startpunkt
für die Beschreibung realistischer Situationen bereitstellen. In jedem
Falle erlaubt die grosse Freiheit bei der Konstruktion solcher Systeme
mitunter eine gewisse einfache Handhabbarkeit. Man nennt solche Modelle
dann auch akademisch. Hier kommt eines.
Das Modell
In einem Volumen V befinden sich N kugelförmige Teilchen mit Durchmesser
sigma. Es gibt zwei Typen von Kugeln, nennen wir diese Typen positiv (+)
und negativ (-). Die potentielle Energie zwischen zwei Teilchen beliebigen
Typs verschwindet, wenn beide Teilchen nicht überlappen, d.h. wenn
ihr Abstand r grösser als der Kugeldurchmesser sigma ist. Überlappen
zwei Kugeln vom gleichen Typ (++ oder --) so ist das energetisch
ungünstig, es liefert einen Beitrag +epsilon (epsilon>0) zur Gesamtenergie.
Sind die überlappenden Teilchen von unterschiedlichem Typ (+- oder
-+), so ist das energetisch günstig, sie wechselwirken mit der
Energie -epsilon.
Man sieht, diese Wechselwirkung hat die gleiche Symmetrie die einer
Mischung positiver und negativer Ladungen innewohnt - gleiche Typen stossen
sich ab, ungleiche Typen ziehen sich an. Die funktionale Form der Ortsabhängigkeit
ist aber eine andere. Statt dem 1/r-Gesetz beim Coulombpotential haben
wir hier eine Stufenfunktion.
Die Frage (und ihre Geschichte)
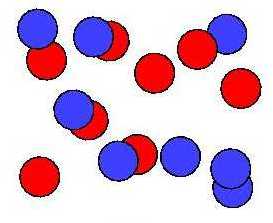 |
Man dachte anfangs, das Modell hätte eine flüssige Phase, wo die Teilchen sich im ganzen Volumen frei bewegen können. |
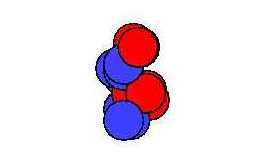 |
Doch dann stellte sich heraus, dass das System kollabiert zu einem einzigen Cluster, der alle Teilchen aufsaugt. (Man sieht das an einer quadratisch mit der Teilchenzahl anwachsenden negativen potentiellen Energie.) |
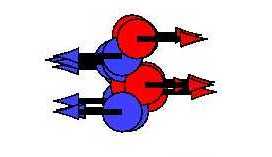 |
Dann erkannte man den Zusammenhang mit der Zweistrom-Instabilität. Was würde passieren, wenn man an den Teilchen in entgegengesetzter Richtung ziehen würde? (Der Pfeil an einer Kugel zeigt die Kraft, die auf sie wirkt.) |
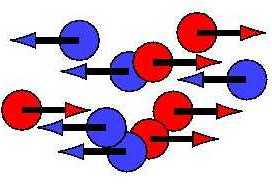 |
Löst sich dann der Cluster auf und gibt es eine flüssige Phase, in der beide Teilchensorten homogen durcheinander durchströmen? |
Aufgaben
- Wie lautet die potentielle Energie des Systems in Formeln?
- Verifiziere den Kollaps. Berechne dazu die Energie der im zweiten Bild gezeigten Konfiguration. Nimm vereinfachend an, dass jeweils N/4 gleiche Teilchen überlappen.
- Erweitere vorhandenen Monte-Carlo-Simulationscode dieses Modells auf Brownsche Dynamik mit Drift.
- Führe Simulationsläufe für sinnvolle Parameter durch.
- Triff mittels geeigneter Grössen Aussagen darüber, ob und wie der Kollaps von der Drift beeinflusst wird.
Bemerkung
Für erfolgreiche Teilnahme am Praktikum sind Aufgaben eins bis
vier ausreichend. Aufgabe eins und zwei sind Vorbereitung, Aufgabe drei
unter Anleitung, Aufgabe vier eigenverantwortlich.




