Institut für Theoretische Physik II: Weiche Materie - HHU Düsseldorf
Fortgeschrittenen-Praktikum: Weiche Materie - Archiv - Dynamik mit Hanteln
Dynamik mit Hanteln
Motivation
Kolloidale Suspensionen bestehen oft aus kugelförmigen Teilchen, die
in einer Flüssigkeit schweben. Diese Suspensionen können so präpariert
werden, dass sie über lange Zeiträume hinaus stabil sind. Ein
Prozess der Instabilität, der eine Suspension gleichsam zerstört,
ist das Zusammenklumpen der Teilchen. Man spricht von Koagulation. Sie
rührt von der van-der-Waals Anziehungskraft der Teilchen aufeinander
her. (Das Potential dieser Anziehungskraft hat eine negative Divergenz
beim Kontakt der Teilchen!)
Die Koagulation ist oft der Feind der Kolloidwissenschaftler, denn das
vormals suspendierte Material fällt nun aus der Lösung aus. Man
kann aber den Spiess umdrehen, den Feind zum Freund verwandeln, und sich
gerade für die Eigenschaften von Koagulation und koagulierten Kolloiden
interessieren. Wir tun das für den Fall von koagulierten Pärchen,
die die Form von Hanteln besitzen.
Auswertung
Die Arbeit von Marcus Heide zur Huepfenden Hantel (postscript,
486kB) behand(t)elt die Physik der hier gestellten Aufgabe.
Modell
Betrachte ein Kugel-Dimer:. Das sind zwei Kugeln mit Durchmesser sigma
im Abstand sigma voneinander. Der Abstand ist dabei fest. Das Dimer soll
eine gleichförmige Massendichte haben. Es sei einem gleichförmigen
Gravitationspotential ausgesetzt und befinde sich über einer ebenen
Platte (Reagenzglasboden).
Spekulation
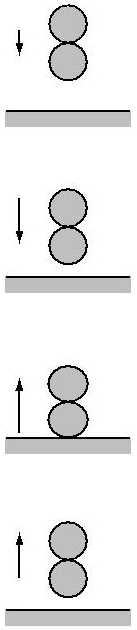
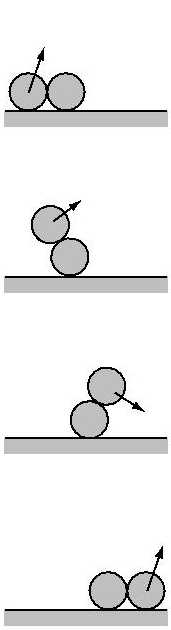
Denkbar sind die folgenden typischen Bewegungsformen. Insbesondere
die dritte Mode sollte man mal mit zusammengeklebten Tischtennisbällen
auf einer Tischplatte (Ha, das ist also der wahre Ursprung!) ausprobieren.
-Durchaus überraschend. (Pfeile symbolisieren Geschwindigkeiten.)
| Miteinander hüpfen | Aufeinander hüpfen | Sich überschlagen |
 |
 |
 |
Aufgaben
- Welche Eigenschaft verbindet die oben gezeigten Bewegungen? Welche der drei sind stabil, welche instabil? Gibt es weitere mit der gefragten Eigenschaft?
- Wie lauten die klassischen Bewegungsgleichungen des Modells? Wie lautet die Brownsche Dynamik dafür? Wie lauten die Bewegungsgleichungen im Übergangsbereich zwischen klassischer zu Brownscher Dynamik?
- Berechne mit Hilfe geeigneter Korrelationsfunktionen durch numerische Integration der Bewegungsgleichungen die statistischen Eigenschaften des Systems. Was sind dafür geeignete Korrelationsfunktionen?
Bemerkung
Aufgabe eins und die erste Frage von Aufgabe zwei ist Vorbereitung.
Die zweiten Teil von Aufgabe zwei und drei in Zusammenarbeit mit dem Betreuer.
Der erste Teil von Aufgabe drei in Zusammenarbeit mit Betreuer oder eigenverantwortlich.




