Institut für Theoretische Physik II: Weiche Materie - HHU Düsseldorf
Fortgeschrittenen-Praktikum: Weiche Materie - Archiv - Milch und Mayo Lösung
Emulsionströpfchen als zweidimensionale ausgerichtete Ellipsen
Das Problem wird hier 2-dimensional mittels Monte-Carlo-Simulation
gelöst. Die Öltröpchen sind Ellipsen mit einer Exzentrizität
kleiner als 1. Im Gegensatz zu den ursprünglichen Ellipsoiden ist
nun die potentielle Energie der Ellipsen nicht proportional zur Oberfläche
sondern zum Umfang der Ellipsen. Die Wechselwirkung der Ellipsen untereinander
ist hart.
Zur Berechnung des Umfangs der Ellipsen wird anstelle des vollständigen
elliptischen Integrals zweiter Gattung E(e,p/2) eine
Näherungsformel verwendet (s. Funktion Umfang() in oel.cpp).
Diese Näherungsformel liefert auch für grosse Exzentrizitäten
noch Werte, die sehr wenig vom Ergebnis des elliptischen Integrals abweichen.
Die Eingaben
Das Programm oel.cpp benötigt einige
Angaben, die der Benutzer frei wählen kann:
Zunächst kann man sich entscheiden ob man zwei Werte für
die Halbachsen der beiden gleichgroßen Ellipsen oder deren Flächen
angeben möchte. Es ist bei der dann u.U. folgenden Eingabe der Größen
der Halbachsen egal welche der beiden die große und welche die kleine
sein soll. Die Werte werden ohne Maßeinheiten angegeben.
Das Programm benötigt ferner den Parameter beta. Dieser ist der
Quotient aus Oberflächen -
spannung bzw. hier "Längenspannung" und thermischer Energie (k
* T).
Die Anzahl der Variationen gibt die Anzahl der gleichzeitigen Veränderungen
der Länge der Halbachsen und des Schwerpunktsabstands an.
Der maximale Abstand der Schwerpunkte bestimmt in welchem Bereich der
Schwerpunkts - abstand vom Programm variiert werden kann.
Die letzte Eingabe gibt die Grenze vor um die die Längen der Halbachsen
maximal zwischen zwei Rechenschritten variieren können.
Der Programmablauf
Nach der Eingabe der Daten bestimmt das Programm einen
zufälligen Startabstand der Schwerpunkte der Ellipsen. Dann wird falls
möglich als Länge der beiden Halbachsen der Radius eines Kreises
mit dem Flächeninhalt einer Ellipse vorgegeben. Ist dies wegen eines
Überlapps nicht möglich so startet das Programm mit zwei sich
berührenden Ellipsen.
Während der nun folgenden Schleifen werden die Längen
der Halbachsen der beiden Ellipsen unabhängig voneinander variiert.
Als Ausgangslänge für die Variation dient die Ursprüngliche
Länge der Halbachse einer Ellipse. Dagegen wird ein neuer Abstand
der Schwerpunkte zufällig aus dem Intervall gewählt, dessen obere
Grenze der maximale Schwerpunktsabstand ist.
Überlappen sich die Ellipsen in der neuen Konfiguration
so wird automatisch die alte Konfiguration als neue Konfiguration gewählt
(Überlapp verboten).
Andernfalls wird über die Annahme der neuen Konfiguration
mit Hilfe des Metropolis - Algorithmus entschieden.
Am Ende einer solchen Schleife wird überprüft
in welchem, der zu Beginn des Programms bestimmten Schwerpunktsintervalle,
sich der Schwerpunktsabstand der neuen Konfiguration befindet. Für
dieses Intervall wird dann die Häufigkeit um 1 erhöht. Die Anzahl
der zu überprüfenden Intervalle kann im Quelltext mit Hilfe der
Konstanten Z verändert werden.
Zu guter Letzt werden die mittleren Energien und Umfänge
in den Intervallen bestimmt.
Die Ausgaben
Das Programm oel.cpp liefert vier Dateien:
| Ellipse.dat: | Diese Datei enthält die absoluten Häufigkeiten dafür, daß sich der Schwerpunkt der Ellipsen im Abstand d in einem der oben genannten Intervalle befindet. |
| lnEllip.dat: | Diese Datei liefert den negativen Logarithmus der absoluten Häufigkeiten. |
| Energie.dat: | Diese Datei liefert die mittlere Energie der Ellipsen im Schwerpunktsabstand d. |
| Umfang.dat: | Diese Datei liefert den mittleren Umfang der Ellipsen im Schwerpunktsabstand d. |
Ergebnisse
Im folgenden werden die Ergebnisse für drei verschiedene Werte von beta graphisch dargestellt.
Für beta wurden die Werte 0.1, 1 und 10 gewählt.
In allen drei Fällen wurde als Fläche der Ellipsen F=3.14259
und als maximaler Schwerpunktsabstand d_max=4 bestimmt. Die Anzahl der
Variationen betrug 1000000 und die maximale Veränderung der Länge
der Halbachsen pro Variation betrug 5 % des maximalen Schwerpunktsabstands.
Der maximale Schwerpunkts - abstand wurde in 50 Intervalle aufgeteilt.
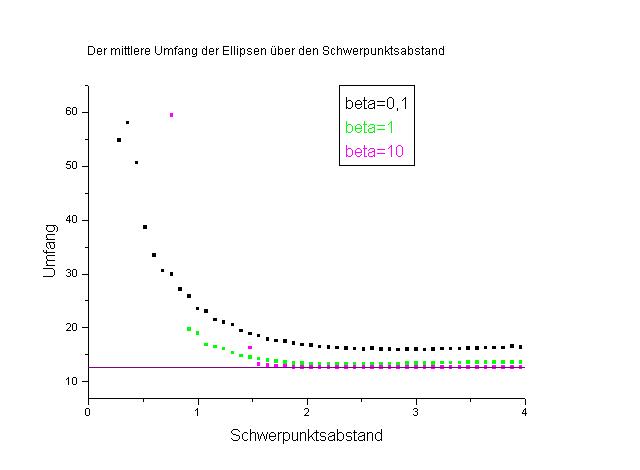
Zunächst wird der mittlere Umfang der Ellipsen in Abhängigkeit
des Schwerpunktsabstands eingetragen. Der Umfang eines Kreises, das ist
der kleinstmögliche Umfang einer Ellipse, ist als unterer Grenzwert
als Linie ebenfalls in das Diagramm eingetragen worden.
Man erkennt deutlich, daß ein großes beta in Schwerpunktsabständen
größer als zwei nur eine geringe Formfluktuation zuläßt.
Der Umfang ist dann annähernd der eines Kreises. Dagegen scheint der
Umfang der Ellipsen für kleine beta relativ stark zu fluktuieren.
In allen Fällen tendiert der Umfang der Ellipsen für große
Abstände gegen einen konstanten Wert. Für kleine Abstände
werden die Ellipsen wegen der harten Wechselwirkung zunehmend elliptischer.
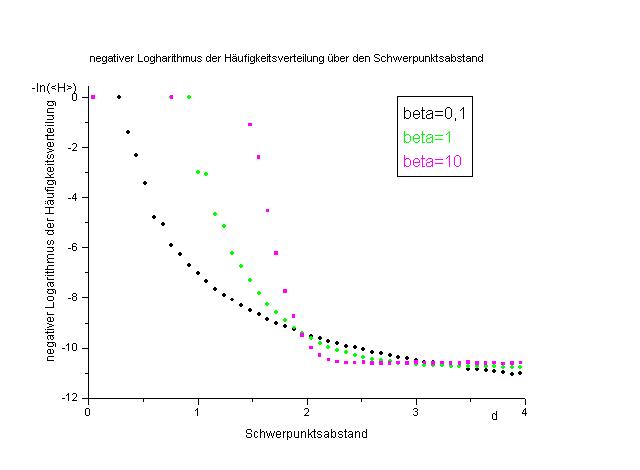
In der nächsten Graphik ist der negative logarithmus der absoluten
Häufigkeiten über den Schwerpunktsabstand aufgetragen. Man erhält
dadurch eine Vorstellung über den qualitativen Verlauf des effektiven
Wechselwirkungspotentials zwischen zwei fluktuierenden Ellipsen.
Man erkennt deutlich, daß das effektive Wechselwirkungspotential
für Abstände oberhalb des Abstands 2 am niedrigsten ist. Weiterhin
erkennt man, daß mit geringer werdendem Schwerpunktsabstand und steigendem
beta die effektive Abstoßung der Ellipsen größer wird.
Man findet in diesem Diagramm auch die Erklärung weshalb im ersten
Diagramm für kleine Abstände und beta=10 der mittlere Umfang
der Ellipsen scheinbar größer als in den anderen beiden Fällen
ist. Für die beiden Fälle ist die absolute Häufigkeit=1
und die Werte ergeben sich wahrscheinlich durch die Startkonfiguration
der Ellipsen.
Quellcode des Programms oel.cpp.
Zurück zu Milch und Mayo.
10.12.98
Marco Wischmeier