Institut für Theoretische Physik II: Weiche Materie - HHU Düsseldorf
Fortgeschrittenen-Praktikum: Weiche Materie - Archiv - Nadeln entlang einer Linie
Nadeln entlang einer Linie
 |
| Flüssigkristall. Die kurzen Nadeln repräsentieren die Moleküle eines Flüssigkristalls. Diese verfügen ueber Rotations- und Translationsfreiheitsgrade. In unserem einfachen Modell können sich die Teilchen entlang einer Linie bewegen und sich in der Bildebene drehen. Die Konfiguration ist ein Schnappschuss aus einer Computersimulation (A. Esztermann, A. Posth). Dazu auch Filme (mpeg, 1.5MB und mpeg, 1.8MB) und Ergebnisse (ps, 342kB). |
Motivation
Flüssigkristalle werden von nicht-kugelförmigen Molekülen
oder kolloidalen Teilchen gebildet. Man kan sich stäbchenförmige
Partikel vorstellen, die sich gegenseitig abstossen. Einfrieren passiert
in solchen Systemen über eine ganze Kaskade von Phasenübergängen.
Die auftretenden Phasen vereinen Eigenschaften von Flüssigkeiten und
Eigenschaften von Festkörpern, daher der Name Flüssigkristall.
Die einfachste flüssigkristalline Phase heisst nematische Phase. In
ihr sind die Richtungen der Teilchen eingefroren; die Nadeln deuten also
im Mittel in eine gemeinsame Richtung. Die Schwerpunkte der Teilchen sind
aber, wie in einer Flüssigkeit, völlig ungeordnet. Um theoretische
Ansätze entwickeln zu können, überlegen wir uns:
Was ist das einfachste Modell diskreter Teilchen, die über kontinuierliche
Orientierungs- und Positionsfreiheitsgrade verfügen?
Modell
Betrachte N Nadeln der Länge L, die in einer Ebene liegen.
Die Schwerpunkte der Nadeln dürfen sich nur entlang einer eindimensionalen
Linie innerhalb der Ebene bewegen. Die Nadeln seien unendlich dünn.
Die Wechselwirkung der Nadel untereinander sei "hard-core", d.h., keine
zwei Nadeln dürfen sich kreuzen.
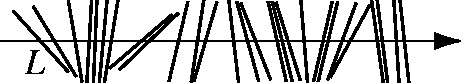
Aufgaben
- Wie lautet die Überlapp-Bedingung für zwei Teilchen in obigem Modell?
- Berechne den zweiten und, wenn möglich, den dritten Virialkoeffizienten.
- Berechne die Orientierungsverteilungsfunktion in Abhängigkeit von der Dichte mittels Monte-Carlo oder Molekular-Dynamik-Simulation.
- Berechne dynamische Korrelationen mit Molekular-Dynamik-Simulation.
Bemerkung
Aufgaben eins und zwei sind Vorbereitung. Aufgabe vier ist optional.
Auswertung
Nadeln entlang einer Linie, (postscript, 342kB) A. Esztermann, A. Posth
Zur Monte-Carlo Simulation dieses Modells:
Film1, (mpeg 1.5MB) und Film2,(mpeg 1.8MB), A. Esztermann




